Voyons maintenant les systèmes possédant 2 plans [miroirs]. Si ils sont parallèles, on obtiendra une série de transformations qui seront des translations et des symétries.

            Le cas général est avec des plans sécants. Nous nous retrouverons donc avec des transformations qui pourront être des rotations et des symétries. Si l'angle des deux plans est w, le produit des deux symétries planes est une rotation d'angle 2w. Le groupe contient donc toutes les rotations d'angle 2mw où m est un entier. En général ce groupe sera infini; il sera fini s'il existe une valeur de m telle que 2mw = 2n (pi). Dans ce cas on a un groupe fini de rotations et symétries d'ordre 2k et on sait qu'alors l'angle minimum de deux plans de symétrie est (pi)/k. Ce groupe peut être engendré par les symétries par rapport à ces deux plans.

            Voyons le cas avec 3 plans. Si ces 3 plans passent par le même point, alors c’est un kaléidoscope sphérique qui sera vu juste après.

            Voyons le cas où les plans sont sécants mais en points d’intersection différents. On obtiendra un triangle où, cas particulier :



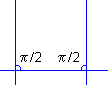
            Dans les autres cas, on obtiendra donc un triangle. Les angles seront inférieurs à (pi)/k (avec k>2) sinon l’angle est obtus.

            Dans un cas général, on cherche avec k, l, m réels < 2 ; (pi)/k+(pi)/l+(pi)/m = (pi) car la somme des angles d’un triangle vaut (pi).

            Supposons 2 <= k < l < m. Cette équation admet les solutions (2, 3, 6), (2, 4, 4) et (3, 3, 3).



            Voici ce que donneraient les plans de profil. On place un point P dessus pour continuer le raisonnement.


Si P est sur la bissectrice de 2 miroirs [plans] alors le polygone créé sera un polygone régulier.

Le point P a 7 positions possibles : soit sur un sommet, soit au bout d'une bissectrice, soit à l'intersection des bissectrices.